Unlike the matrix case, computing low-rank approximations of tensors is NP-hard and numerically ill-posed in general. Even the best rank-1 approximation of a tensor is NP-hard. In this paper, we use convex optimization to develop polynomial-time algorithms for low-rank approximation and completion of positive tensors. Our approach is to use algebraic topology to define a new (numerically well-posed) decomposition for positive tensors, which we show is equivalent to the standard tensor decomposition in important cases. Though computing this decomposition is a nonconvex optimization problem, we prove it can be exactly reformulated as a convex optimization problem. This allows us to construct polynomial-time randomized algorithms for computing this decomposition and for solving low-rank tensor approximation problems. Among the consequences is that best rank-1 approximations of positive tensors can be computed in polynomial time. Our framework is next extended to the tensor completion problem, where noisy entries of a tensor are observed and then used to estimate missing entries. We provide a polynomial-time algorithm that requires a polynomial (in tensor order) number of measurements, in contrast to existing approaches that require an exponential number of measurements for specific cases. These algorithms are extended to exploit sparsity in the tensor to reduce the number of measurements needed. We conclude by providing a novel interpretation of statistical regression problems with categorical variables as tensor completion problems, and numerical examples with synthetic data and data from a bioengineered metabolic network show the improved performance of our approach on this problem.

Statistical and Computational Results

A. Aswani (2016), Low-rank approximation and completion of positive tensors, SIAM Journal on Matrix Analysis and Applications, vol. 37, no. 3: 1337-1364.

Supplementary Code

MATLAB Code Impelementation of the five tensor completion methods (including two new methods) compared in the above paper.

Synthetic Data

Entries were uniformly sampled from the tensor
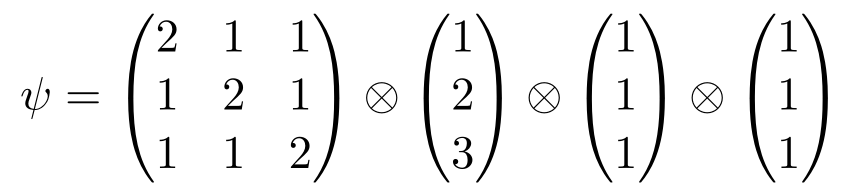and the measurement noise had a gamma distribution. Five methods for tensor completion were compared at two different noise levels, and the table below shows that the (sparse) partition log-linear models perform competitively against existing approaches. More details and citations can be found in the above paper.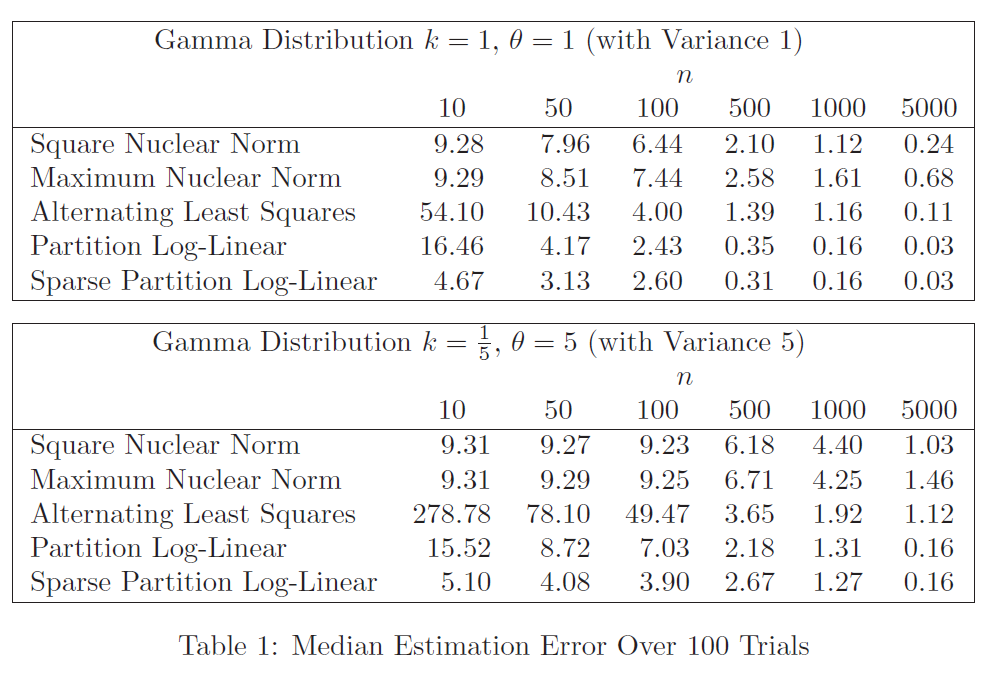

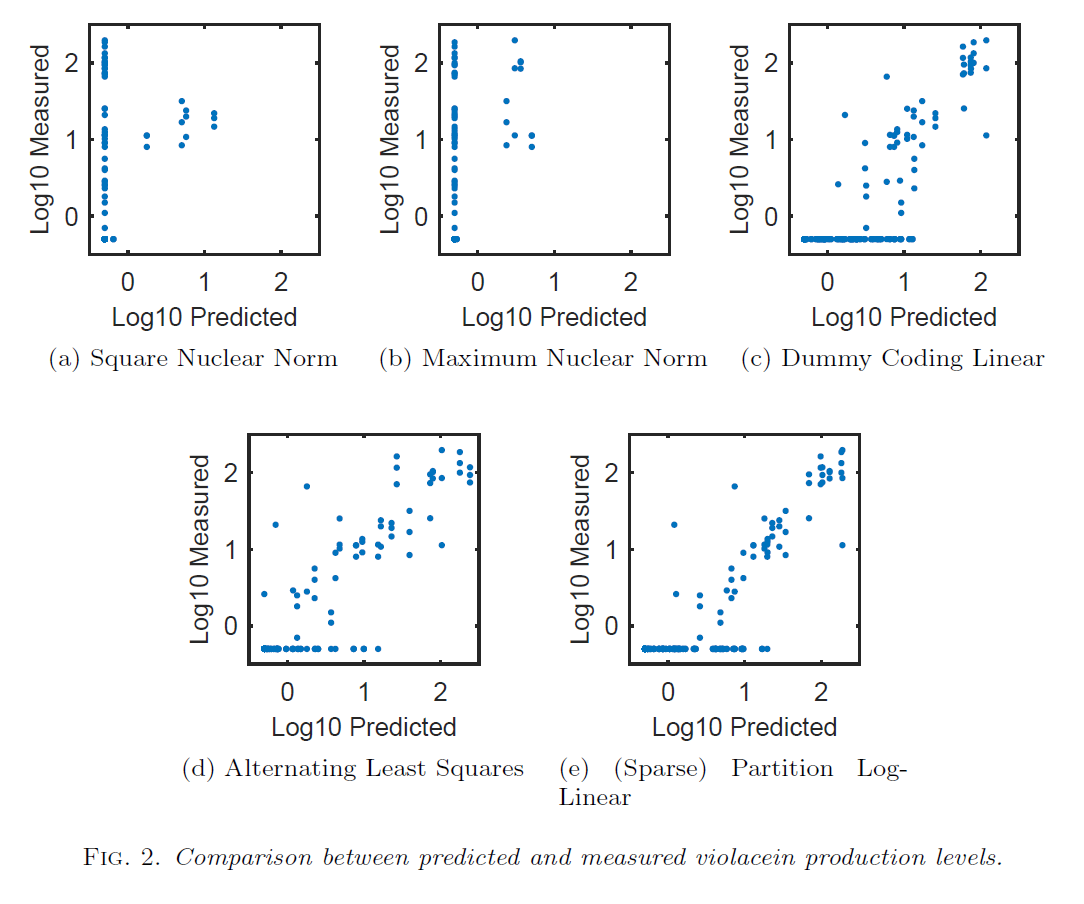
Violacien Pathway

Many bioengineered metabolic pathways can be modeled by a combinatorial regression model. Using data collected from the violacein pathway, several different methods for constructing combinatorial regression models were compared. The predictions of the (sparse) partition log-linear model most closely match the experimentally observed quantities, having a higher Spearman correlation coefficient than a dummy coding linear model and three models computed using the maximum and square nuclear norms and alternating least squares. Plots of the model predictions versus experimentally measured concentrations are shown below, and more details and citations can be found in the above paper.